dBmとは何か? その2

R&Dセクションの永井です。
以前、電波を取り扱うときに出てくる「dBm」について取り上げてみました。
今回はdBmを使うメリットについて考えていきたいと思います。
dBmのメリットは計算のしやすさにあると思います。
計算機の無かった時代はもちろん、現代でも手計算や暗算を使って概算をするときに便利です。
また、計算が容易になると、計算ミスを減らすこともできます。
dBmはdBの一種で、1mWを基準としたものですが、ここで考えるメリットは何が基準であっても変わらないので、以下では一般的にdBのメリットとして見ていきます。
なお、dBm(dB)がどういうものかについては、以前のブログでその概要を取り上げていますので、そちらをご参照ください。
今回は以前に取り上げた内容をご存じだという前提で話を進めます。
>> 前回のブログ「dBmとは何か?」
桁数を少なく表現できる
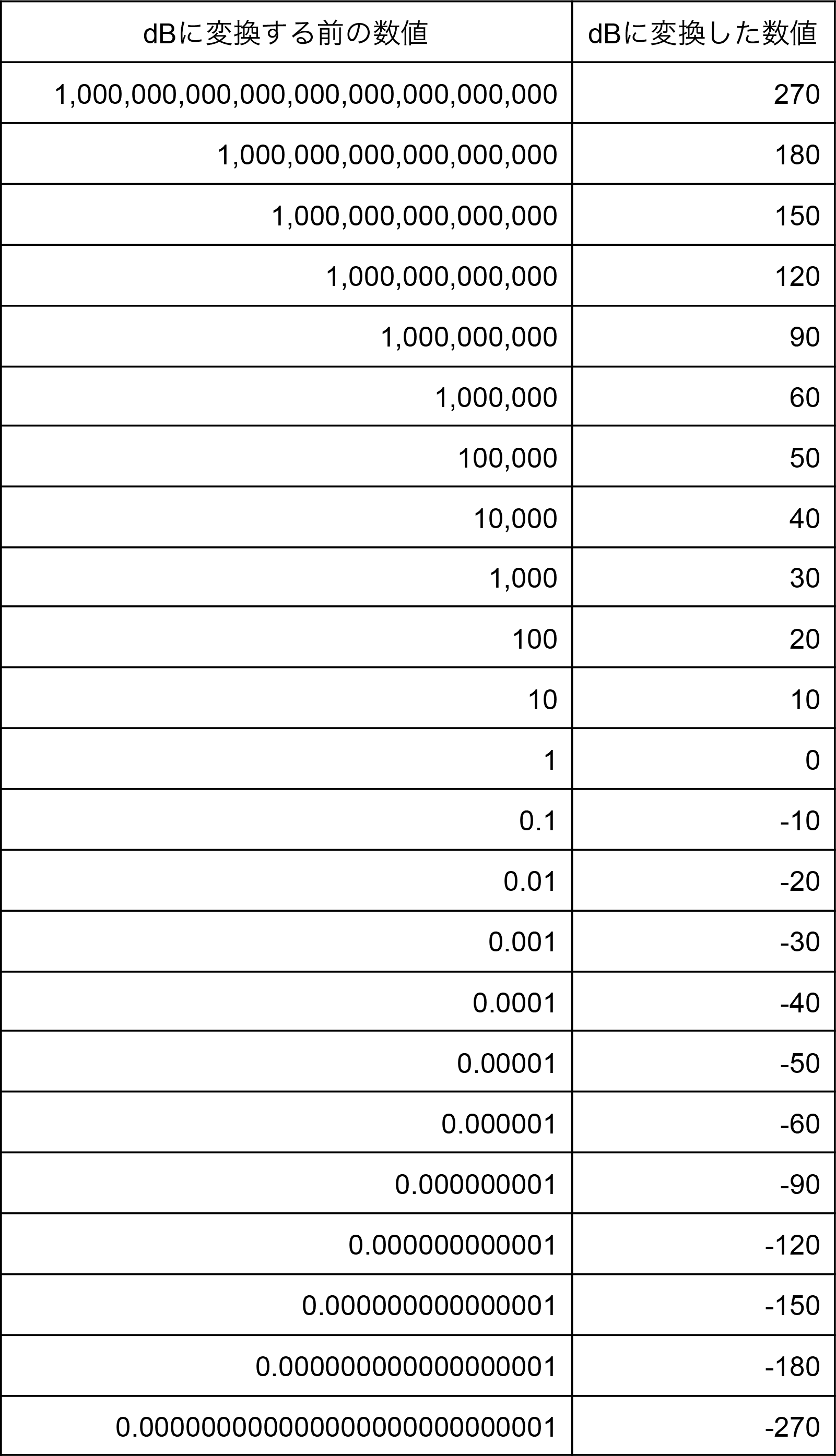
ひとつ目は、dBを使うと桁数の大きな数値から小さな数値までをほぼ一定の桁数で表記できるというメリットです。
大きな数値でも小さな数値でもdBに変換すると、1桁~3桁の範囲に収めることができます。(これは必要に応じて、小数点以下を四捨五入した結果です。)
なお、dBに変換すると、1より大きい数値は正の数、1の時は0、1より小さい数値は負の数になります。
上の例は0が並んだピッタリした数値ですが、次はそうでない例です。
(dBに変換した数値は小数点以下を四捨五入しています。)
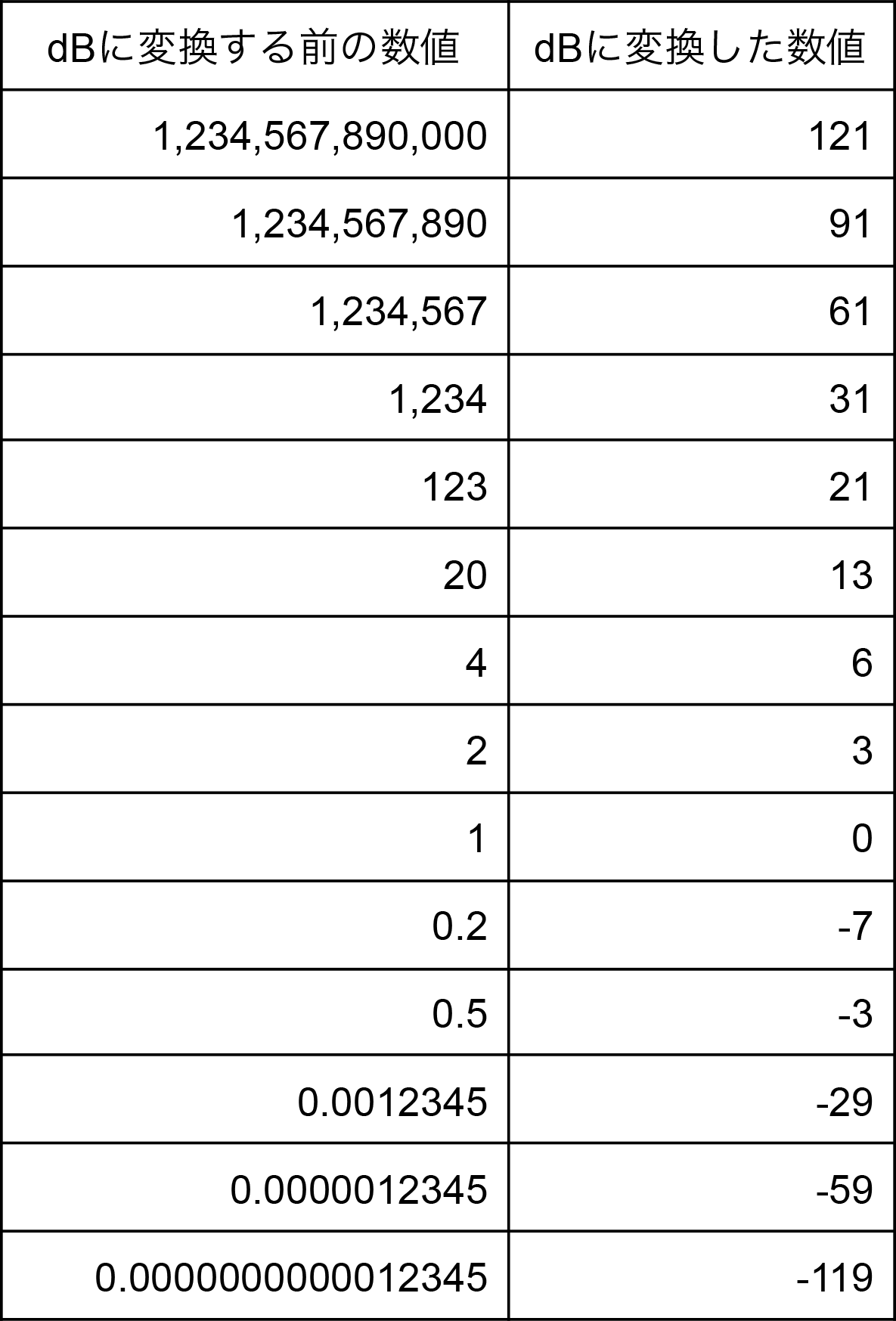
このように、大きな数値から小さな数値までを扱わないといけないとき、dBに変換すると1桁~3桁の整数で表現できるため、手計算による概算が容易になります。
掛け算と割り算を足し算と引き算として計算できる
dBに変換すると、掛け算と割り算をそれぞれ足し算と引き算として計算することができます。
次の掛け算(1)と足し算(2)は同じ計算をしています。
(60dBを変換すると、1,000,000になります。)
![]()
![]()
これには次のような仕組みがあります。
(1)を書き換えると、
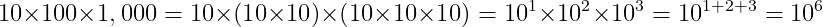
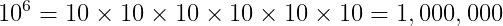
になります。
10を何回掛けているかを示すために10の右肩に書く数字を指数といいます。
掛け算すると指数の部分は足し算されます。
この指数を取り出して、10倍したものがdBです。
よって、dBによる計算は、指数の計算である
![]()
の数値をそれぞれ10倍にして実行したものだといえます。
すなわち、
![]()
という計算です。
この60dBを元の数値に戻すと、1,000,000になります。
同じように、次の割り算(3)と引き算(4)は同じ計算をしています。
(30dBを変換すると、1,000になります。)
![]()
![]()
これには次のような仕組みがあります。
(3)を書き換えると、
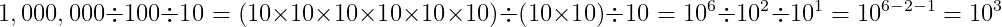
![]()
になります。
割り算をすると指数の部分は引き算されます。
掛け算のときと同様に、dBによる計算は、指数の計算である
![]()
の数値をそれぞれ10倍にして実行したものだといえます。
すなわち、
![]()
という計算です。
この30dBを元の数値に戻すと、1,000になります。
このように、dBは元の数値を10の指数で表した数値(を10倍したもの)ですので、通常の数値による掛け算と割り算が指数の足し算と引き算になっているという性質を使えます。
この性質があるので、特に1つの計算で多くの掛け算や割り算を繰り返す場合(信号の増幅や減衰)、dBを用いると計算が容易になります。
その他の例
(5)と(6)は同じ計算をしています。
![]()
![]()
23dBを変換すると、ほぼ200(199.5・・・)です。
(7)と(8)も同じ計算をしています。
![]()
![]()
75dBを変換すると、おおよそ31,622,777です。
結果にそれなりの差がありますが、正確さを求めない概算であれば、使用可能だと思います。
dBへの変換計算で10倍する理由
最後にdBに変換するときに10倍する理由を考えてみます。
これも計算を容易にすることと関係しています。
上に掲載した例をもう一度掲載しますが、ここではdBの計算に10倍を入れなかった場合の数値も掲載しています。
(10倍しない場合はdBの最初の「d(デシ)」がなくなり、Bになります。)
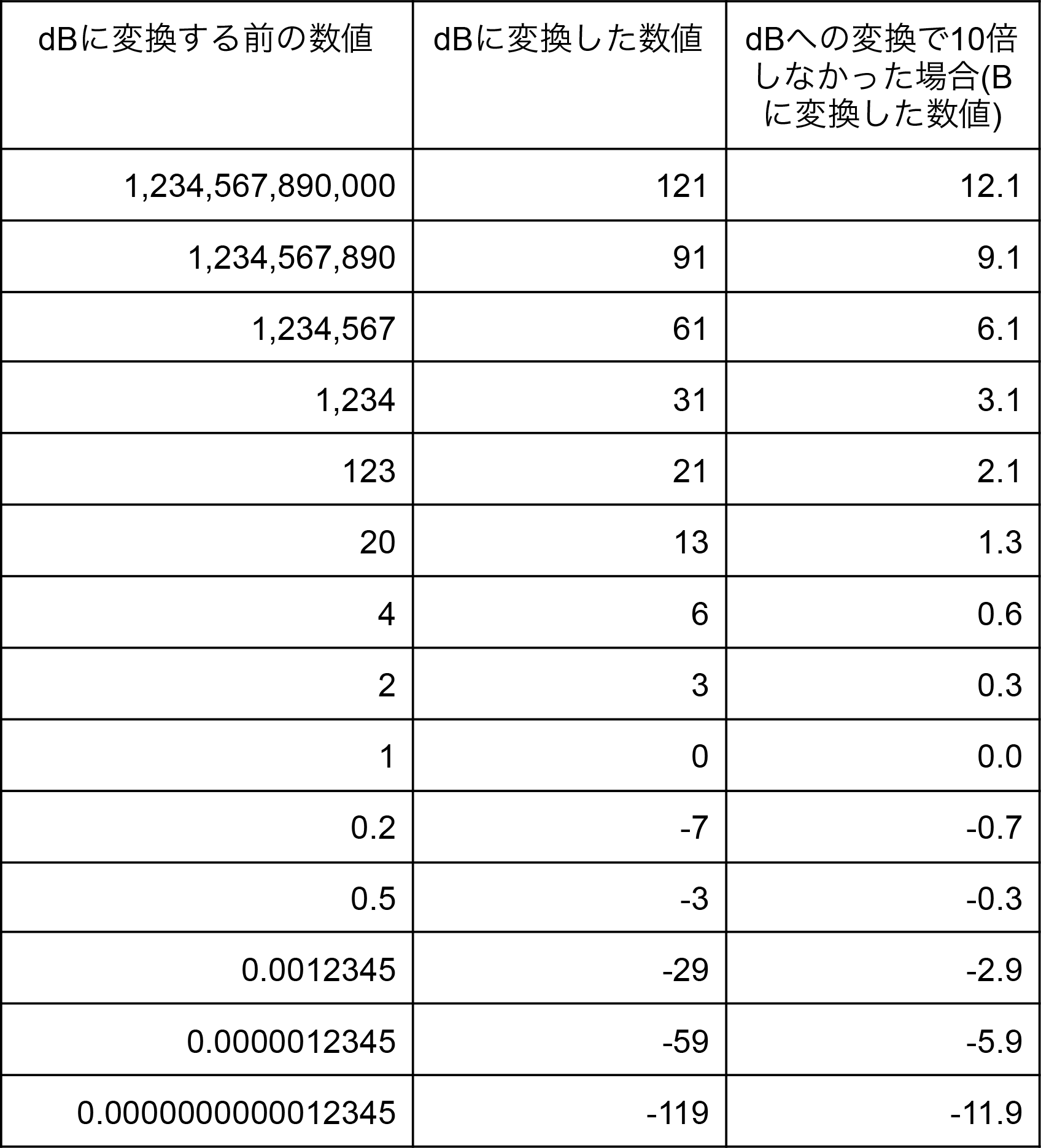
10倍した数値の方が計算しやすそうだということ(特に手計算や暗算)が分かると思います。
小数点以下に数字があると、計算が面倒です。
12.1や9.1といった数値は、精度は落ちますが、12と9に丸めて計算することもできます。
しかし、0.3や-0.7のような数値で同じようにするとかなり精度が悪くなります。(1, 0, -1のどれかになります。)
しかもこの辺りの数値はよく使う範囲でもあるので、精度が悪いのはあまりよいことではありません。
やはり、10倍にしておいた方がよさそうです。
このような理由からdBに変換するときに10倍するようになったと思われます。
以上、dBm(dB)のメリットを見てきました。
どれも計算のしやすさに関係しており、計算機が無かった時代には重要なことでした。
一方、計算機が発達した現代でも、特に手書きや暗算による概算をするとき、便利に使えます。


 ブログ
ブログ