dBmとは何か?

R&Dセクションの永井です。
今回は電波を取り扱うときに出てくる「dBm」について取り上げます。
RFIDなどの電波の強さを表すのにdBm(デシベルミリワット)という単位が使われます。
弊社製品のスペック表にも、RFIDの送信出力として「30dBm」や「24dBm」といった記載があります。
このdBmがどういうものなのか調べてみました。
電波の強さは電力で表され、単位はW(ワット)やその千分の一を表すmW(ミリワット)を使うことが多いです。
1Wや250mWのように表現します。
この電波の強さを別の方法で表現するときに使う単位がdBmです。
30dBmや24dBmのように表現します。
結論から言うと、dBmは電波の強さが1mW(基準とする値)の何倍になるかを求め、その常用対数を計算して、10倍した値を表します。
これでは分かりにくいので、dBmを分解して、詳しく見ていきます。
その1
dBmの真ん中の文字Bは常用対数を計算することを意味しています。
このBはベルと読み、実用的な電話機を発明したアレクサンダー・グラハム・ベルの名前に由来します。
まず、常用対数を理解するため、次のことを考えてみます。
100は10を2回かけたもので、これを10の2乗と表現します。
同じく1000は10を3回かけたもので、これを10の3乗と表現します。
そして、10それ自体は10の1乗と表すことができます。2乗や3乗は10の右肩に小さい数字を書いて表します。

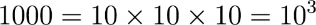
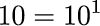
また、1は10の0乗と決められています。
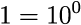
さらに、1より小さい数についても10の何乗かで表現することができます。
この場合、何乗の値がマイナスになると決められていて、0.1は10の-1乗、0.01は10の-2乗、0.001は10の-3乗と表現します。
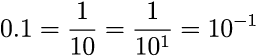
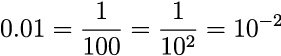
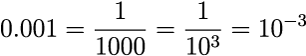
上の例は何乗の値がピッタリ整数になるものばかりです。
しかし、整数にならないもの(無限小数など)も含めると、様々な数を10の何乗かで表すことができます。
例えば、7は10の約0.845乗、123は10の約2.09乗、0.2は10の約-0.699乗になります。
(関数電卓でlog計算をすると簡単に求められます。)
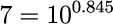
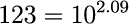
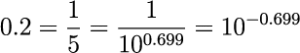
以上を踏まえて、ここから常用対数です。
数値x(エックス)の常用対数y(ワイ)を計算する式は次のように表現されます。
(log(ログ)とその右下の小さい10は常用対数の計算を表す記号と考えます。)
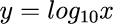
この式において、yはxが10の何乗であるかを表します。
逆に考えると、10のy乗がxになります。
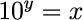
例えば、
xが100のとき、100は10の2乗なので、yは2になります。
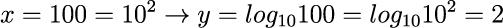
xが7のとき、7は10の0.845乗なので、yは0.845になります。
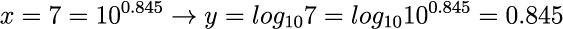
xが1のとき、1は10の0乗なので、yは0になります。
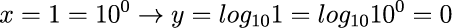
xが0.001のとき、0.001は10の-3乗なので、yは-3になります。
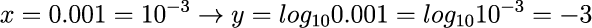
まとめると、B(ベル)はある数値xの常用対数yを計算することを意味します。
その2
次にdBmの最初の文字dです。
このdはデシと読み、十分の一を表す接頭辞です。
1mg(ミリグラム)のm(ミリ)がg(グラム)の千分の一を表したり、
1cm(センチメートル)のc(センチ)が1m(メートル)の百分の一を表すのと同じです。
1L(リットル)の十分の一は1dL(デシリットル)になります。
1LをdLで表す場合、10倍して10dLとします。
同じく、B(ベル)で表される常用対数yをdB(デシベル)で表される値zに変換する場合、yを10倍すればよいことになります。
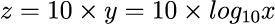
(zの単位はdB、yの単位はB)
このdBは電波の強度以外にも様々な量や比を表すのに使われています。
電波の強さを表現するdBmもdBの使い方のひとつです。
その3
最後にdBmの最後の文字mです。
このmはmW(ミリワット)のことで、電波の強さと1mWの比(1mWの何倍か、何分の一か)をとることを表しています。
電波の強さをP(単位はWまたはmW)とすると、
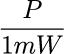
例えば、
電波の強さPが1W(1000mW)なら、1mWの1000倍になります。
電波の強さPが250mWなら、1mWの250倍になります。
電波の強さPが1mWなら、1mWの1倍になります。
電波の強さPが0.2mWなら、1mWの0.2倍(五分の一)になります。
その4
ここまでdBmの3つの文字をそれぞれ見てきましたが、これらを合わせて考えてみます。
m(ミリワット)
電波の強さP(単位はWまたはmW)と1mWの比を求め、これをxとします。
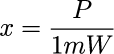
B(ベル)
電波の強さPと1mWの比xの常用対数yを計算します。
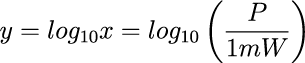
d(デシ)
常用対数yを10倍し、これをzとします。
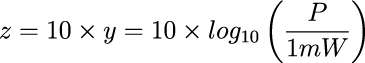
この計算結果であるzの単位がdBmになります。
このように、dBmは電波の強さが1mW(基準とする値)の何倍になるかを求め、その常用対数を計算して、10倍した値を表します。
計算の例を示します。
電波の強さPが1W(1000mW)の場合、1mWの1000倍になります。
1000は10の3乗だから、常用対数は3となり、これを10倍します。
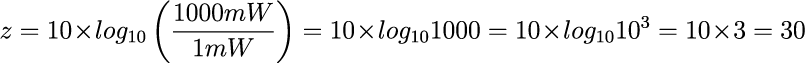
よって、電波の強さ1Wは30dBmに変換できます。
電波の強さPが250mWの場合、1mWの250倍になります。
250は10の約2.4乗だから、常用対数は約2.4となり、これを10倍します。
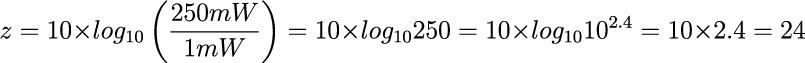
よって、電波の強さ250mWは24dBmに変換できます。
電波の強さPが1mWの場合、1mWの1倍になります。
1は10の0乗だから、常用対数は0となり、これを10倍します。
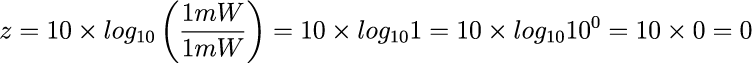
よって、電波の強さ1mWは0dBmに変換できます。
電波の強さPが0.2mWの場合、1mWの0.2倍になります。
0.2は10の約-0.699乗だから、常用対数は約-0.699となり、これを10倍します。
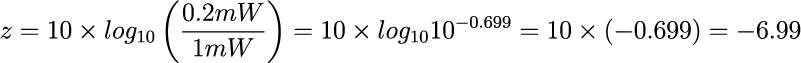
よって、電波の強さ0.2mWは-6.99dBmに変換できます。
これらの例からもわかりますが、
電波の強さPが1mW(基準値)より大きいとき、dBmは0よりも大きい値(プラスの値)になり、
電波の強さPが1mW(基準値)と同じとき、dBmは0になり、
電波の強さPが1mW(基準値)より小さいとき、dBmは0よりも小さい値(マイナスの値)になります。
その5
実際にmWとdBmを変換するときは関数電卓やパソコンを使うと便利です。
mWからdBmへの変換
関数電卓の場合、数値(単位はmW)を入力して、「LOG」ボタンを押して、10倍すれば求められます。
エクセルの場合、関数「LOG(数値)」に数値(単位はmW)を代入して、10倍すれば求められます。
250(mW)なら、「=10*LOG(250)」と入力 →23.9794(dBm)
dBmからmWへの変換
関数電卓の場合、数値(単位はdBm)を0.1倍して、下のボタンで計算すると求められます。
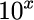
エクセルの場合、関数「10^(数値)」に0.1倍した数値(単位はdBm)を代入すれば求められます。
24(dBm)なら、「=10^(24/10)」と入力 →251.1886(mW)
その6
以上、dBmという単位について見てきました。
一見、複雑そうですが、原理がわかれば、それほどむずかしいものではないと思います。
ただ、次のような疑問がまだあります。
なぜ電波の強さをわざわざdBmで表すのでしょうか。
なぜBmを10倍したdBmを使っているのでしょうか。
これらはまた機会があれば、取り上げてみたいと思います。


 ブログ
ブログ